 |
 |
| Physiology? | Figures & Illustrations | Test Questions | Daily Quiz | Calculators | Physiology Tutor | Glossary |
 |
 |
 |
 |
 |
 |

Resting Membrane Potential -
Membrane Ionic Current Equations
Membrane Ionic Current Equations
As we have seen before, physiological solutions contain a high concentration of ions (see here). The major cation in the extracellular fluid is sodium (Na+) and the major anion in the extracellular fluid is chloride (Cl−). The major cation in the intracellular fluid is potassium (K+) while the major anions in the intracellular fluid are inorganic and organic anions (see Ionic Composition of Body Fluids). Since ions are charged species, they can carry electrical current in solutions. When ions traverse the permeation pathway of an ion channel from one side of the membrane to the other side, their movement generates an ionic current that can be measured by using electrophysiological methods.
Electrophysiology is the application of electrical measurements to physiological systems. Our understanding of the function of many physiological phenomena has been advanced solely or mostly through the use of electrical measurements. We learned earlier in this lecture that electrophysiological methods can be used to measure the potential difference across the plasma membrane (see Resting Membrane Potential - Introduction). Similarly, when ions cross the membrane via any pathway (whether the pathway is an ion channel, transporter, or pump), an electrical current is generated and can be measured via the use of electrophysiological methods. Even more importantly, even when direct electrical measurements of physiological parameters are not possible (e.g., motion or force generation), the signals can be converted into electrical signals by using transducers (e.g., a force transducer). In these cases, electrical measurements become excellent proxy measurements of the physiological processes under investigation. Therefore, as students of physiology and biology in general, it is important that you gain a basic understanding of the principles underlying electrical phenomena.
Ohm's law
As mentioned above, movement of ions in solutions leads to the generation of electrical currents. The current carried by ions can be examined in much the same way as current is measured in electrical circuits. Ohmís law (Equation 1) describes the relationship between the current, the imposed electrical field, and the resistance to current flow in the system:
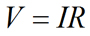 |
Eq. 1 |
where V is the voltage (in volts), I is current (in Amperes, or simply Amps), and R is the resistance (in Ohms, Ω) to current flow. For an ion (charged species) passing through an ion channel, its flow (or current, I) is influenced by the electrical field across the membrane (Vm) and the resistance to flow (R) through the ion channel. A larger potential difference across the plasma membrane leads to a larger current flow. Moreover, a smaller resistance to flow leads to a larger current flow. It can also be readily seen that if there is no potential difference across the plasma membrane (i.e., Vrest = Vm = 0), there will be no net ion flow (i.e., I = 0) at the resting membrane potential regardless of the value of resistance to ion flow. Equation 2 represents a rearrangement of Ohm's law and shows how the voltage across the membrane and resistance to ion flow can influence the current carried by an ion.
 |
Eq. 2 |
Often, it is helpful to use a graphical approach to view the relationship between current flow and voltage. Such a relationship is referred to as a current-voltage relationship, current-voltage curve, or current-voltage plot (see Fig. 1 below). It may also be simply called an I-V relationship, I-V curve, or I-V plot. For use in biological research and in relation to the movement of ions across biological membranes, current is carried by the movement of ions across the membrane through pores or pathways created by membrane transport proteins (channels, transporters, pumps, etc.). Current may also result from ion movement through non-specific pathways. As we have discussed throughout this lecture, the membrane potential may be referred to as Vm. Similarly, the current through the membrane may be referred to as Im, and membrane resistance to ion flow may be referred to as Rm (see Equation 3).
 |
Eq. 3 |

Figure 1. Current-voltage (I-V) relationship.
This figure shows a hypothetical current-voltage (I-V) relationship using Equation 1. Experimentally, such an I-V plot can be obtained by changing the membrane potential to the desired values ranging from −200 to +100 mV and measuring the resulting current values at each voltage. Ohm's law (V = IR) states that the voltage difference across the plasma membrane is equal to the product of membrane current and membrane resistance (Equation 1). In this hypothetical example, it is assumed that the resting membrane potential is zero (Vrest = 0 mV). For the purpose of I-V relationships, Equation 1 may be rearranged to obtain Equation 2: I = V/R. If current is plotted as a function of the membrane potential, the result is a current voltage (I-V) plot such as the one shown in this figure. Note that when the membrane potential is at the resting membrane potential (i.e., V = Vrest = 0 mV), the current is zero. The slope of this plot is the inverse of resistance (slope = 1/R). In this hypothetical example, the slope reveals a membrane resistance of 1 megaOhms (R = 1 MΩ). Moreover, in this example, the slope is constant at all membrane potential values. The inverse of resistance is conductance (G), which is a measure of the ease with which ions can permeate the membrane.
Current-voltage (I-V) relationships are useful because they allow us to visually see the direction of current flow (and, hence, ion flow) at any given membrane potential. Experimentally, I-V curves are determined by establishing a desired voltage across the membrane by using voltage-clamp electrophysiological techniques, where the membrane voltage is experimentally adjusted and the resulting current values at each voltage are recorded. A typical voltage range for an I-V curve is −150 mV to +50 mV to ensure that the physiological voltage range is covered. Figure 1 shows a hypothetical I-V relationship, where the membrane potential is experimentally varied between −200 and +100 mV. In this hypothetical example, it is assumed that the resting membrane potential is zero (Vrest = 0 mV). It can be seen from the plot that when the voltage is at the resting membrane potential (V = Vrest = 0 mV), the current is zero (I = 0). It can also be seen that the slope of the I-V plot can be used to determine the membrane resistance (R) to ion flow (because R = V/I). In this hypothetical example, the slope of I-V plot reveals a membrane resistance of 1 megaOhms (R = 1 MΩ).
Often, instead of examining the "resistance to current flow" (resistance, R), we speak of the "ease of current flow", which is called conductance (G). Conductance is simply the inverse of resistance (Equation 4) and is a measure of the ease with which current can flow in the system. The unit of conductance is Siemens. When considering biological membranes, conductance refers to the pathways in the membrane that allow ions to permeate the membrane, and is a measure of the ease with which ions can permeate these pathways. As noted above, these pathways may be specific (e.g., ion channels, transporters, pumps, etc.), or they may be non-specific.
 |
Eq. 4 |
Considering Equation 4, and substituting for R in Equation 2, we obtain:
 |
Eq. 5 |
where I is current (in Amperes), G is conductance (in Siemens), and V is voltage (in Volts). This equation also demonstrates that the slope of a current-voltage plot is equal to conductance (see Fig. 1). Equation 5 also makes it obvious that in order to have a current that is carried by an ion, an electrical field (voltage) must be acting on the ion and, in addition, there must be pathways in the membrane that allow the ion to pass through (for example, ion channels).
An ionic pathway may refer to specific ion channels. The ease with which an ion permeates the pore of a single ion channel is referred to as the single-channel conductance (also referred to as unitary conductance or microscopic conductance). It is the conductance of a single channel. The single-channel conductance can be measured by using a specialized form of electrophysiological methods referred to as the patch clamp technique. However, for any given ion, we can also measure the conductance of the entire plasma membrane for that ion. In this case, the conductance is the macroscopic conductance for a given ion. The macroscopic conductance is simply the product of the single-channel conductance and the total number of channels in the plasma membrane. By convention, single-channel parameters are depicted by lower case letters, and macroscopic parameters are depicted by capital letters. Therefore, g is the single-channel conductance and G is the macroscopic conductance. G = Ng, where N is the total number of channels in the membrane.
It is readily seen that if the channels for an ion are closed (i.e., G = 0), the current carried by that ion will be zero (i.e., I = 0), regardless of how many channels are present in the membrane. Moreover, it can also be seen that if no electrical field acts on an ion (i.e., V = 0), the current carried by that ion will be zero (i.e., I = 0), regardless of how many channels are present in the membrane even if all those channels are open.
Application of Ohm's law when the resting membrane potential is not zero
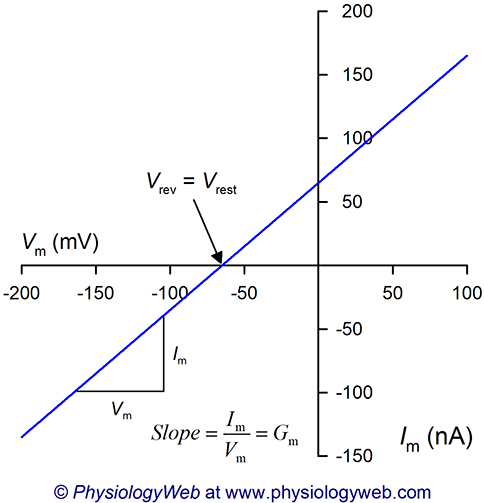
Figure 2. Current-voltage (I-V) relationship when the resting membrane potential is not zero.
This figure shows a hypothetical current-voltage (I-V) relationship based on Equation 6: Im = Gm(Vm − Vrest). Experimentally, such an I-V plot can be obtained by changing the membrane potential to the desired values ranging from −200 to +100 mV and measuring the resulting current values at each voltage. In this example, it is assumed that Vrest = −65 mV. Note that the slope of the plot is the membrane conductance (Gm). Here, it is assumed that Gm is constant at all voltages tested, however, we will see in future lectures that membrane conductances often vary with the membrane potential. Also note that when the membrane potential (Vm) is equal to the resting membrane potential (Vrest), the current is zero. Thus, the zero current level, also known as the reversal potential (Vrev), occurs when the membrane potential is at the resting membrane potential (Vrev = Vrest = −65 mV).
So far, we have discussed the Ohm's law mainly in general terms without specifically addressing the fact that there is usually a non-zero resting potential difference across the plasma membrane of cells. When we take this fact into account, Equation 5 can be rewritten to give Equation 6:
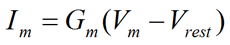 |
Eq. 6 |
where Im is the membrane current (in Amperes), Gm is the membrane conductance (in Siemens), Vm is the membrane potential (in Volts), and Vrest is the resting membrane potential (in Volts). It can be seen that the magnitude of the current carried through the membrane (Im) depends on the magnitude of the difference between Vm and Vrest (Vm − Vrest) as well as the magnitude of the membrane conductance (Gm). At the molecular level, the membrane conductance (Gm) is a function of the total number of open channels in the membrane. It is readily seen that if the membrane potential is at the resting membrane potential (Vm = Vrest), there would be no net current through the membrane (Im = 0) (see Fig. 2).
When examining current-voltage (I-V) relationships, the membrane voltage at which the direction of current changes from negative (i.e., inward) to positive (i.e., outward) is called the reversal potential (Vrev). The reversal potential simply refers to that membrane voltage at which there is no net current across the membrane (i.e., I = 0). Thus, at Vrev, there is no net ionic movement across the plasma membrane.
Figure 2 shows a hypothetical I-V plot assuming that Vrest = −65 mV and that Gm is constant at all voltages tested. Note that the zero current level (i.e., reversal potential) in Fig. 2 is at the resting membrane potential (Vrev = Vrest = −65 mV). Therefore, at Vrest, there is no net current flow across the plasma membrane. By extension, we can state that at Vrest, there is no net movement of ions across the plasma membrane.
Ohm's law applied to the movement of specific ions across biological membranes
We now turn our attention to applying Ohm's law to the movement of specific ions across the plasma membrane of cells. We know that for any given ion, there is an equilibrium potential that is likely not equal to the resting membrane potential. Therefore, the net force acting on an ion is not simply the potential difference across the plasma membrane. Rather, it is the net driving force discussed previously in this lecture (Driving force = Vm − VEq.) (see Electrochemical Driving Force Acting on Ions). When we take this into account, the current equation can now be rewritten as Equation 7:
 |
Eq. 7 |
where I is current carried by an ion (in Amperes), G is conductance for the ion (in Siemens), Vm is the membrane potential (in Volts), and VEq. is the equilibrium potential for the ion (in Volts). Recall that the difference between Vm and VEq. is the driving force that acts on the ion (Driving force = Vm − VEq.). The direction of movement of the ion will depend on the ionic species and on the arithmetic sign (i.e., positive or negative) of the driving force (Vm − VEq.). The direction of current flow (carried by the ionic species) will depend on the charge carried by the ion (see Table 1). The magnitude of the current carried by the ionic species will depend on the magnitude of the driving force (Vm − VEq.) as well as the magnitude of conductance for that ion (G). At the molecular level, conductance (G) is a function of the total number of open channels for a given ion.
Table 1. Sign of electrochemical driving force (VDF), sign of current, and direction of ion flow
| Ionic species | Sign of driving force (VDF = Vm − Veq.) |
Sign of current | Direction of ion flow |
| Cation | + 0 − |
+ 0 − |
Outward No net flow Inward |
| Anion | + 0 − |
+ 0 − |
Inward No net flow Outward |
+ refers to VDF > 0, − refers to VDF < 0, and 0 refers to VDF = 0. When VDF = 0, the ion is in electrochemical equilibrium. The sign of VDF also determines the sign of current. Cation, positively-charged ion; Anion, negatively-charged ion; Outward, ion movement out of the cell; Inward, ion movement into the cell.
Equation 7 can be written for any ion of interest. For example, the current equation for Na+ is: INa = GNa(Vm − VNa). The current equation for K+ is: IK = GK(Vm − VK). The current equation for Cl− is: ICl = GCl(Vm − VCl). In a similar fashion, the current equation can be written for any other ion of interest.
The convention in physics is that current is the flow of positive charge. But it should be remembered that in solutions, current is carried by either cations or anions. Using Table 1 and a knowledge of the equilibrium potential for any given ionic species, it is possible to determine the direction of flow for that ion at a given membrane potential. For example, assume that VK = −100 mV and Vm = −70 mV. Thus, the driving force acting on potassium is DFK = [−70 − (−100)] = +30 mV. The sign of the driving force is positive. When this is multiplied by GK, it results in a positive value for IK. Remember that conductance is always positive and cannot have a negative value. Since K+ is a positively charged ion, a positive current value indicates that K+ is flowing out of the cell (see Table 1). For convenience, we have created a driving force calculator that can help determine the direction of ion flow across the membrane.
As a second example, if VCl = −65 mV, using the same reasoning, you should be able to conclude that at Vm = −70 mV, Cl− ions move out of the cell (remember that chloride is an anion). In this case, the driving force acting on Cl− is DFCl = [−70 − (−65)] = −5 mV. You should do this calculation for K+, Na+, Cl−, and Ca2+ at a variety of different membrane potentials until it becomes second nature to you and you begin to intuitively appreciate it.
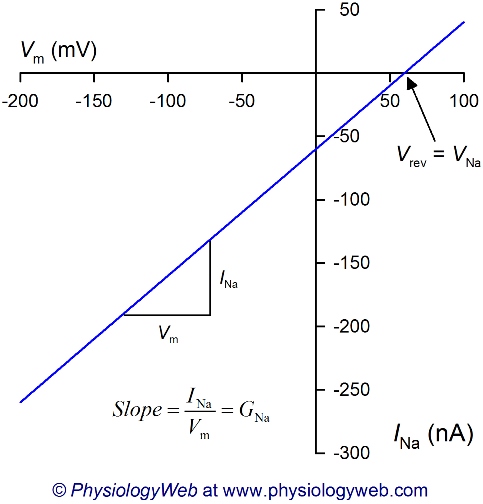
Figure 3. Current-voltage (I-V) relationship for sodium ion (Na+).
This figure shows a hypothetical current-voltage (I-V) relationship for Na+ ion based on Equation 7: INa = GNa(Vm − VNa). Experimentally, such an I-V plot can be obtained by changing the membrane potential to the desired values ranging from −200 to +100 mV and measuring the resulting current values at each voltage. Note that the slope of the plot is the conductance for sodium (GNa). Here, it is assumed that GNa is constant at all voltages tested, however, we will see in future lectures that ion conductances often vary with the membrane potential. Also note that when the membrane potential (Vm) is equal to the sodium equilibrium potential (VNa), the current is zero because no driving force acts on Na+ ions at that membrane potential (DFNa = Vm − VNa = 60 − 60 = 0 mV). Thus, the zero current level, also known as the reversal potential (Vrev), is equal to the sodium equilibrium potential (Vrev = VNa). Na+ flows out of the cell at all voltages more positive than VNa (because DFNa and INa are positive), and Na+ flows into the cell at all voltages less than VNa (because DFNa and INa are negative). See text and Table 1 for details.
Figure 3 shows a current-voltage relationship for Na+ and is a graphical representation of Equation 7 for the current carried by Na+ (INa) as Na+ across the plasma membrane. A comparison of Figures 1, 2, and 3 reveals that the zero level current (i.e., reversal potential, Vrev) occurs at a different membrane potential. In Figure 3, the zero current level is at the equilibrium potential for Na+ (VNa = 60 mV) because at this potential, the driving force acting on Na+ ions is zero (DFNa = Vm − VNa = 60 − 60 = 0 mV). Examination of Equation 7 shows that if the driving force is zero, no net movement of the ion can take place across the plasma membrane (regardless of the magnitude of the ion conductance). At all voltages other than VNa, a driving force acts on Na+ ions, and the sign of the driving force determines the direction in which Na+ ions flow across the plasma membrane (into or out of the cell). For example, at Vm = 0 mV, a large negative driving force acts on Na+ ions (DFNa = 0 − 60 = −60 mV). A negative driving force leads to a negative value of INa at 0 mV (Fig. 3). Therefore, using Table 1 and knowing that Na+ is a cation, it can be determined that at 0 mV, Na+ ions flow into the cell. By using a similar reasoning, we can see that Na+ flows out of the cell at all voltages more positive than VNa (because DFNa and INa are positive), and Na+ flows into the cell at all voltages less than VNa (because DFNa and INa are negative).
Similarly, I-V plots for K+, Cl−, Ca2+, or any other ion would reveal that the reversal potential (Vrev) is at the equilibrium potential for that ion (not shown).
To summarize, for an ion to carry current across the plasma membrane, two requirements must be met. First, there must be a driving force acting on the ion. Therefore, the potential difference across the membrane must be different from the equilibrium potential of the ion (Vm ≠ VEq.). Second, there must be channels specific to that ion in the plasma membrane and the channels must be open (G ≠ 0). The direction of current flow depends on the direction of the driving force and the nature of the ion (anion or cation; see Table 1). The magnitude of the current depends on the magnitude of the driving force, as well as the magnitude of the conductance for the ion (i.e., total number of open channels in the membrane).
If there is only one ion in the system and channels specific to that ion are open, the reversal potential is the same as the equilibrium potential for that ion (see Fig. 3). For example, if only potassium-specific channels are open, then the reversal potential will be the same as VK. So if only potassium channels are open, then Vrev = Vrest = VK. In this case, Vrev can be obtained directly from the Nernst equation (see also Nernst equation calculator). On the other hand, if channels for K+, Na+, and Cl− are open, then Vrev = Vrest, where Vrest is determined either from the Goldman-Hodgkin-Katz equation (see also GHK equation calculator) or the chord conductance equation. However, in this case, Vrest is not equal to VK, VNa, or VCl. Figure 2 provides an example of this situation.
Posted: Saturday, February 15, 2014
Last updated: Wednesday, November 22, 2017
Last updated: Wednesday, November 22, 2017