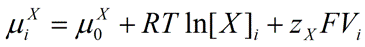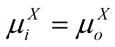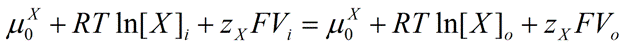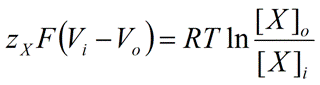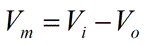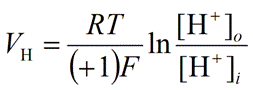Derivation of the Nernst Equation
The Nernst equation describes the electrochemical equilibrium distribution of an ion between two compartments that are separated by a membrane that contains channels selective for that ion. In an ideal case, the membrane separating the two compartments allows only the passage of the ion of interest and no other ion. The distribution of the ion across the membrane is governed by the ion concentration gradient across the membrane and leads to the establishment of a potential difference across the membrane. At equilibrium, this potential difference is described by the Nernst equation, and is referred to as the equilibrium potential (Veq.) or Nernst potential for that ion.
The Nernst equation can be derived based on simple thermodynamic principles
The Nernst equation can be derived by considering the differences in chemical potential and electrical potential between two solutions that are separated by a membrane that contains selective ionic channels. Figure 1 demonstrates the two compartments and the biological membrane separating the two compartments. Since our ultimate goal is to use the Nernst equation for biological cells, we will designate one compartment as i (for inside of the cell) and the other as o (for outside of the cell), corresponding to the intracellular and extracellular compartments, respectively. For the purpose of this derivation, we will assume that the membrane contains ionic channels that are selective for the ionic species X. We will further assume that no other types of ionic channels exist in the membrane separating the two compartments. Therefore, if X crosses the membrane through ion channels selective for X, its counter-ion Y cannot follow due to a lack of selective channels for Y.
Our goal is to define the total chemical potential for ionic species X on each side of the membrane. Therefore, we will define μiX for the total chemical potential of X inside the cell, and μoX for the total chemical potential of X outside of the cell. We will also consider the fact that in addition to the traditionally accepted chemical potential (which is governed by the concentration of the ion; RTln[X]), because of the electrical charge on the ion, an electrical component (zXFV) may contribute to the total chemical potential on each side of the membrane. Thus, our goal is to derive an equation that conveniently describes the electrochemical gradient across the membrane for ion X.
Therefore, the intracellular total chemical potential of ion
X may be defined as:
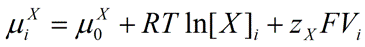 |
Eq. 1 |
where
μiX is the total intracellular chemical potential for ion
X,
μ0X is the standard chemical potential for ion
X,
R is the universal gas constant (8.314 J.K
-1.mol
-1, Joules per Kelvin per mole),
T is temperature on the Kelvin scale (K = °C + 273.15),
[X]i is the intracellular concentration of ion
X,
zX is the valence of ion
X,
F is the Faraday's constant (96485 C.mol
-1, Coulombs per mole), and
Vi is the electrical potential inside the cell. For reasons that are beyond the scope of this discussion, the natural logarithm of the concentration is used (
ln[X]i).
Similarly, we can define the extracellular total chemical potential of ion
X as:
 |
Eq. 2 |
where
μoX is the total extracellular chemical potential for ion
X,
[X]o is the extracellular concentration of ion
X,
Vo is the electrical potential outside the cell, and
μ0X,
R,
T,
zX, and
F have the same meanings noted above. It is important to note that
μ0X has the same value in both solution compartments. It is also important to note that
[X]i and
[X]o should be expressed using the same concentration unit (μM, mM, M, etc.).
At equilibrium, the following condition must be met:
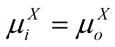 |
Eq. 3 |
Therefore,
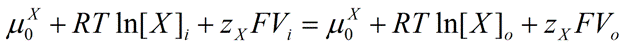 |
Eq. 4 |
Simplifying and rearranging Equation 4, we obtain the following:
 |
Eq. 5 |
Further simplification of Equation 5 yields the following:
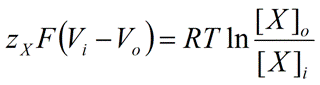 |
Eq. 6 |
The electrical potential difference between the intracellular and extracellular compartments (
Vi − Vo) defines the potential difference across the plasma membrane, simply referred to as the
membrane potential (Vm). We can, therefore, state the following:
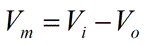 |
Eq. 7 |
Replacing
Vi − Vo in Equation 6 above with
Vm, we obtain the following:
 |
Eq. 8 |
Finally, solving for
Vm, we obtain the
Nernst equation:
 |
Eq. 9 |
Nernst equation for ions of physiological interest
A few examples of the Nernst equation for ions of physiological interest are shown below:
| Sodium ion (Na+) |
 |
Eq. 10 |
| Potassium ion (K+) |
 |
Eq. 11 |
| Calcium ion (Ca2+) |
 |
Eq. 12 |
| Hydrogen ion (Proton, H+) |
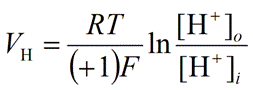 |
Eq. 13 |
| Chloride ion (Cl-) |
 |
Eq. 14 |
Our
Nernst potential calculator can be used along with a knowledge of intracellular and extracellular concentrations to calculate the equilibrium potential (
Veq.) for any ion of interest.
Understanding the Nernst equation
As mentioned above, the Nernst equation determines the
equilibrium potential (Veq.) for an ion. In the ideal case that the membrane contains selective channels only for ion
X, the equilibrium potential (
Veq.) for
X (
VX) defined by the Nernst equation also predicts the potential established across the membrane, simply called the
membrane potential (Vm). Clearly, for this potential to be established across the membrane, selective channels for ion
X must be
present and open. At the equilibrium potential for ion
X, there is no net movement of ion
X because the sum of chemical and electrical forces acting on the ion (i.e., total chemical potential) is the same on both sides of the membrane. Thus, at
Veq. for any ion, there is no net movement of that ion across the membrane. Examination of the Nernst equation reveals that a concentration gradient is also necessary to establish a membrane potential. In the absence of a concentration gradient (i.e., when [
X]
i = [
X]
o),
Veq. = 0. Use the
Nernst potential calculator to perform such calculations.
On the other hand, if additional selective ion channel types are present and are open, the Nernst potential for each ion only determines the equilibrium potential for that ion and no longer predicts the membrane potential. In this case, all ions with selective channels contribute to the value of the membrane potential. The contribution of each ion depends on its concentration gradient across the plasma membrane as well as its relative membrane permeability.
Permeability is the ease with which an ion crosses the membrane and is proportional to the total number of open channels for the ion. When two or more ions contribute to the membrane potential, it is likely that the membrane potential would not be at the equilibrium potential for any of the contributing ions. Thus, no ion would be at its equilibrium (i.e.,
Veq. ≠ Vm). When an ion is not at its equilibrium, an
electrochemical driving force (VDF) acts on the ion, causing the net movement of the ion across the membrane down its electrochemical gradient. The driving force is quantified by the difference between the membrane potential and the ion equilibrium potential (
VDF = Vm − Veq.) (see
Electrochemical Driving Force Calculator). The
Goldman Hodgkin Katz (GHK) equation is used to determine the membrane potential if two or more ions contribute to the membrane potential. For additional details, see the lecture notes on the
Resting Membrane Potential.
Posted: Sunday, June 12, 2011
Last updated: Saturday, February 15, 2014