The temperature coefficient (Q10) represents the factor by which the rate (R) of a reaction increases for every 10-degree rise in the temperature (T). The rate (R) may represent any measure of the progress of a process. For example, the rate may be the velocity of action potential propagation along a nerve fiber (e.g., m/s), or it may be the rate at which the products of a chemical reaction are produced (e.g., mmol/s), or it may be the current (electrical equivalent of ionic flux) conducted through an ion channel, pump, or transporter (e.g., pA, nA, μA, etc.), or it may be the rate at which the heart contracts per minute (i.e., beats per minute, bpm).
 |
 |
 |
 |
 |
In a typical experiment, the rate of the physiological process under investigation is measured at two different temperatures, T1 and T2 (where T2 > T1), thus yielding the rate measurements R1 (measured at T1) and R2 (measured at T2), respectively. The Q10 equation (see below) is then used to estimate the Q10 for the process. The temperature unit must be either the Celsius or the Kelvin, and may not be any other unit, such as the Fahrenheit. Note that T1 and T2 do not need to be exactly 10 degrees apart in order to use this equation. Keep in mind that the same unit must be used for the two temperatures (T1 and T2) at which the rate measurements are obtained. Moreover, the rate measurements (R1 and R2) must have the same unit. Q10 values are useful because they may be used to infer mechanistic insight about the physiological process under investigation (see below).
Temperature Coefficient (Q10) Equation
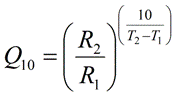
- Q10 is the factor by which the reaction rate increases when the temperature is raised by ten degrees. Q10 is a unitless quantity.
- R1 is the measured reaction rate at temperature T1 (where T1 < T2). Note that R1 and R2 must have the same unit.
- R2 is the measured reaction rate at temperature T2 (where T2 > T1). Note that R1 and R2 must have the same unit.
- T1 is the temperature at which the reaction rate R1 is measured (where T1 < T2). The temperature unit must be either the Celsius or the Kelvin, and may not be any other unit, such as the Fahrenheit. Note that T1 and T2 must have the same unit. T1 and T2 do not need to be exactly 10 degrees apart.
- T2 is the temperature at which the reaction rate R2 is measured (where T2 > T1). The temperature unit must be either the Celsius or the Kelvin, and may not be any other unit, such as the Fahrenheit. Note that T1 and T2 must have the same unit. T1 and T2 do not need to be exactly 10 degrees apart.
Q10 Calculator
Each calculator cell shown below corresponds to a term in the formula presented above. Enter appropriate values in all cells except the one you wish to calculate. Therefore, at least four cells must have values, and no more than one cell may be blank. The value of the blank cell will be calculated based on the other values entered. After a calculation is performed, the calculated cell will be highlighted and subsequent calculations will calculate the value of the highlighted cell (with no requirement to have a blank cell). However, a blank cell has priority over a highlighted cell.
Please note that the unit of temperature used in the above equation must be in Celsius or Kelvin (not Fahrenheit). If your temperature values are in Fahrenheit, please first convert them to corresponding values in Celsius or Kelvin.
Interpretation of Q10
Q10 is a unitless quantity. It is the factor by which the rate increases when the temperature is raised by ten degrees. If the rate of the reaction is completely temperature independent, it can be seen from the equation above that the resulting Q10 will be 1.0. If the reaction rate increases with increasing temperature, Q10 will be greater than 1. Thus, the more temperature dependent a process is, the higher will be its Q10 value. Q10 is ~1 for diffusion of ions and molecules in bulk solutions. For typical chemical reactions, Q10 values are ~2. For many biological processes, particularly those that involve large-scale protein conformational changes, Q10 values are greater than two. Thus, Q10 values may be used to infer mechanistic insight about the physiological process under investigation.
Although the Q10 is a convenient way to examine and report the temperature dependence of a process, it must be kept in mind that a thorough examination of the temperature dependence of a process requires that the rate be measured at more than two temperatures. Typically, the rate of the reaction is measured at multiple (5 or more) temperatures that reasonably represent the relevant physiological temperature range. The data collected are then plotted in an Arrhenius plot, which yields the activation energy (Ea) for the process under investigation. Similar to Q10, Ea is also used to infer mechanistic information about the process, but Ea is thought to be a better approach.
Last updated: Thursday, March 20, 2025






