 |
 |
| Physiology? | Figures & Illustrations | Test Questions | Daily Quiz | Calculators | Physiology Tutor | Glossary |
 |
 |
 |
 |
 |
 |

Neuronal Action Potential -
Na+ and K+ Concentrations Do Not Change during an Action Potential
Na+ and K+ Concentrations Do Not Change during an Action Potential
It is important to note that although during a neuronal action potential, large changes take place in the membrane potential (see figure) as a result of Na+ entry into the cell and K+ exit from the cell (see figure), the actual Na+ and K+ concentrations inside and outside of the cell generally do not change. This is because compared to the total number of Na+ and K+ ions in the intracellular and extracellular solutions, only a small number moves across the neuronal plasma membrane during the action potential. This can be shown by performing a simple calculation (see below). Under rare conditions of continued excitability, however, the concentrations may change a little. It is especially possible that continued excitation along small diameter axons may lead to cytoplasmic concentration changes. It is also possible that the simultaneous activity of many axons in close proximity of one another may bring about a rise in the extracellular K+ concentration. However, in most cases ion concentrations do not change, as the calculations shown below demonstrate.
Below, we will perform a simple calculation in order to assess the extent to which Na+ and K+ concentrations may change during an action potential. Recall that the electrical properties of biological membranes can be modeled by a simple equivalent electrical circuit with a capacitor and resistor in parallel. The capacitor represents the lipid bilayer and is responsible for storing charge across the plsma membrane. The resistor represents the combined ion permeation pathways (i.e., ion channels and transporters) present in the biological membrane. The charge separated across the two plates of a capacitor, or across a biological membrane (see below), can be described by the following relationship:
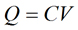 |
Eq. 1 |
where Q is the charge (Coulombs, Coul.), C is the capacitance (Farads, F), and V is the voltage across the capacitor (Volts, V). In the same fashion, the charge separated across the plasma membrane is given by:
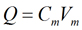 |
Eq. 2 |
where Cm is the specific membrane capacitance and Vm is the membrane voltage. Experiments on many cells and also on artificial lipid bilayers have shown that Cm is approximately 1 μF/cm2 (10−6 F/cm2) in most cells. Although estimates as low as 0.7 μF/cm2 have been proposed, it is usually very convenient to use 1 μF/cm2. Therefore, most investigators use 1 μF/cm2 as the specific membrane capacitance for biological membranes.
If we now assume that during an action potential, approximately a 100-mV change occurs in the membrane potential (actually more than 100 mV from −70 mV to about +40 mV), we can easily calculate the total number of charges that must be separated (moved across the plasma membrane) to cause this 100-mV (0.1 V) shift in Vm. Therefore,
 |
Eq. 3 |
We now need to convert this amount of charge into the total number of ions. Remember that in solutions, charge is carried by ions and that when we are talking about monovalent ions such as Na+ and K+, the charge on one ion is equivalent to 1.6 × 10-19 Coul. (elementary charge). Thus,
 |
Eq. 4 |
The number calculated above refers to the number of ions that must be translocated across 1 μm2 of plasma membrane in order to bring about a 100-mV change in the transmembrane potential. It is better to convert this number to correspond to an area that is more compatible with that of a typical cell. For a cell of about 10 μm in diameter, the surface area (4πr2, where r is the cell radius) of the plasma membrane would be ≈314 μm2. Here, we assume that the cell is a smooth sphere devoid of microvilli. The volume enclosed by this cell (i.e., the cytoplasmic volume; 4πr3/3) is ≈524 μm3. Assuming intracellular Na+ and K+ concentrations of 10 mM and 150 mM, respectively, the cytoplasm of this cell contains 3.2 × 109 Na+ ions and 4.7 × 1010 K+ ions.
With a total surface area of ≈314 μm2, approximately 2,000,000 Na+ ions (314 μm2 × 6,250 ions/μm2 = 1,963,495 ions) enter the cell (spike phase) during a single action potential and, likewise, approximately 2,000,000 K+ ions leave the cell (repolarization phase). A simple comparison of this number with the total number of Na+ ions in the cell shows that the total number of Na+ ions is increased by about 0.06%. This increase is not enough to lead to a significant increase in the macroscopic (bulk) concentration of Na+. Following a similar argument, it can be shown that the relative decrease in the intracellular K+ concentration is even smaller (because the intracellular K+ concentration is much higher).
In summary, during action potentials, Na+ and K+ concentrations do not change. The Na+ ions that enter the cell are too few in number to change the overall (macroscopic) Na+ concentration. Likewise, the K+ ions that leave the cell are few compared to the total number of K+ ions in the cell. Because of the larger volume of the extracellular space, the Na+ and K+ concentrations in this compartment are affected even to a lesser extent. Given enough time, an equal number of Na+ and K+ ions that are translocated during action potentials are moved in opposite directions by the action of the Na+/K+ ATPase. Remember that the turnover rate of this pump (~500 per second) is much slower than that of Na+ and K+ channels (≥ 1,000,000 ions per second). Thus, it takes longer for the pump to return an equal number of ions to their appropriate fluid compartment.
Having considered the calculation shown above, as also mentioned above in the opening to this section, it is possible to envision circumstances in which the Na+ and K+ concentrations may change. When small diameter axons (with small cytoplasmic volume) fire repetitively at high frequency, it is likely that the Na+ and K+ concentrations may change. This final point does not alter the argument put forth against changes in ionic concentrations. It only highlights special cases in which small volumes and rapid firing may lead to changes in Na+ and K+ concentrations.
Posted: Thursday, July 5, 2012
Last updated: Friday, January 17, 2014
Last updated: Friday, January 17, 2014