 |
 |
| Physiology? | Figures & Illustrations | Test Questions | Daily Quiz | Calculators | Physiology Tutor | Glossary |
 |
 |
 |
 |
 |
 |

Hill Equation - Interactive Graph
When studying biochemical or physiological processes, it is often necessary to measure the rate at which a given reaction or process proceeds to completion. Examination of the rate of reactions often provides very useful insight regarding reaction mechanism. For example, studying the rate of an enzyme-catalyzed reaction or the rate of a carrier-mediated transport process as a function of the substrate concentration generally reveals insight about the nature of ligand binding to the protein (enzyme or transporter). For some reactions, the rate increases in a hyperbolic fashion as the substrate concentration increases (see Michaelis-Menten equation). Yet for other reactions, the rate increases in a sigmoidal manner as the substrate concentration increases (see Fig. 1 below).
For hyperbolic reactions, when the substrate concentration is low, the reaction rate increases almost in a linear fashion with increasing substrate concentration. However, as the substrate concentration is increased to higher and higher levels, the reaction rate no longer increases in proportion to the increase in substrate concentration. Thus, at higher substrate concentrations, the reaction no longer increases in a linear manner. Rather, increases in the substrate concentration lead to progressively smaller and smaller increases in the reaction rate. In fact, at very high substrate concentrations, the rate begins to asymptote to a steady-state level, and additional increases in the substrate concentration do not lead to an increase in the reaction rate (see figure). This type of relationship is referred to as hyperbolic and demonstrates saturation of the enzyme or transporter at high substrate concentrations. Saturation is caused by the fact that there is a fixed number of enzyme or transporter molecules, each with a fixed number of substrate binding sites. At high substrate concentrations, all of the binding sites have substrate bound and each enzyme or transporter molecule is working as fast as its intrinsic rate to catalyze the reaction (for enzymes) or transport the substrate across the membrane (for transporters).
Reactions that exhibit a sigmoidal curve also exhibit saturation at high substrate concentration (see Fig. 1 below). However, at low substrate concentrations, a very different behavior is observed (compared to a hyperbolic relationship). At low substrate concentrations, the rate increases only incrementally with increases in the substrate concentration. As the substrate concentration increases further, small increases in the substrate concentration lead to large increases in the reaction rate. At very high substrate concentrations, the rate exhibits saturation, where additional increases in the substrate concentration no longer increase the reaction velocity. This type of saturation kinetics is adequately described by the Hill equation.
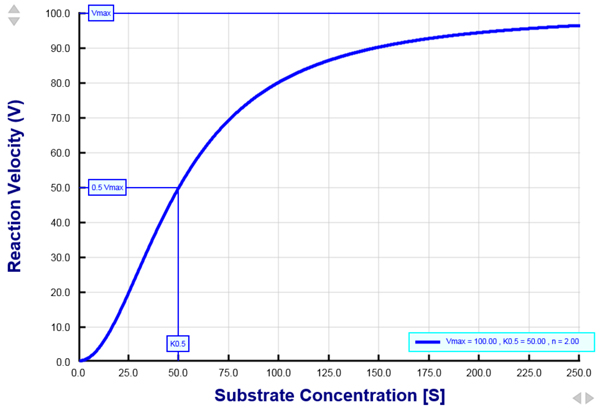
Figure 1. A plot of the reation velocity as a function of the substrate concentration as described by the Hill equation.
When examined at different substrate concentrations, the rate of many enzyme-catalyzed reactions, or the rate of many carrier-mediated transport processes across biological membranes, exhibit a sigmoidal shape. This type of saturation kinetics is adequately described by the Hill equation. Vmax is the maximum reaction velocity. K0.5 is the half-maximal concentration constant and is the substrate concentration that gives rise to 50% Vmax. For this plot, the Hill coefficient (n) was set to 2. The sigmoidal nature of the relationship signifies the existence of substrate binding cooperativity among two of more substrate binding sites in the protein under study.
The Hill equation (see below) is commonly used to study the kinetics of reactions that exhibit a sigmoidal behavior. The rate of many enzyme-catalyzed reactions and many transporter-mediated processes can be analyzed by the Hill equation. Typically, the reaction rate (or reaction velocity) is experimentally measured at several substrate concentration values. The range of substrate concentrations is chosen such that very low reaction rates as well as saturating rates are measured. A plot of the reaction rate versus the substrate concentration reveals three important kinetic parameters: Vmax, K0.5, and n (see Fig. 1). Vmax is the maximum reaction rate that is observed at saturating substrate concentrations. Vmax is a function of the intrinsic turnover rate of the enzyme or transporter as well as a function of the total number of enzyme/transporter molecules that give rise to the measured rate. K0.5 is the half-maximal concentration constant and is the substrate concentration at which the reaction rate is exactly half of Vmax. K0.5 is inversely related to the apparent affinity of the enzyme/transporter for its substrate. Therefore, a low numerical value of K0.5 refers to a very high affinity of interaction between the protein and its substrate. This is because it takes a very small amount (i.e., low concentration) of the substrate to reach 50% of the saturating concentration. Conversely, a high numerical value of K0.5 is indicative of a low affinity of the enzyme/transporter for its substrate. This is because it takes a large amount (i.e., high concentration) of the substrate to reach 50% of the saturating concentration. Thus, K0.5 is a very useful parameter by which the affinity of the protein for various substrates can be compared. n is the Hill coefficient and provides a measure of the cooperativity of substrate binding to the protein. An n value of greater than 1 (n > 1) suggests that two or more binding sites exist in the protein and that there is positive cooperativity with respect to substrate binding. Positive cooperativity refers to a scenario when the binding of one substrate facilitates the binding of another substrate to the protein. If the Hill coefficient is equal to 1 (n = 1), the Hill equation is reduced to its simpler form known as the Michaelis-Menten equation. In this case, there is no substrate binding cooperativity, and is indicative of either a single substrate binding site in the protein, or multiple binding sites that do not interact cooperatively. For this reason, the Hill coefficient is generally not a good indicator of the number of binding sites. The Hill coefficient is a good indicator of the number of binding sites only when there is a very high degree of cooperativity among the sites. Finally, if the Hill coefficient is less than 1 (n < 1), there is negative cooperativity with respect to substrate binding.
It is important to emphasize that the kinetics of transport for many transport proteins exhibit features that are very similar to those of enzymes. Similar to enzymes, transporters show specificity with respect to the substrate transported and, in addition, the rate of substrate transport across a biological membrane exhibits saturation at high substrate concentrations. Therefore, the kinetics of many transport processes can be studied by using the Hill equation or the Michaelis-Menten equation. The Michaelis-Menten equation can adequately describe the dependence of transport rate on the substrate concentration for facilitative transporters, secondary active transporters (cotransporters and exchangers), and primary active transporters (i.e., pumps).
Hill equation
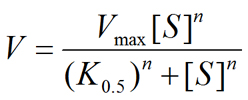
- V is the reaction velocity (rate of reaction progression per unit time) and may be expressed in many different forms such as mmol/s, mol/min, etc.
- Vmax is the maximum velocity of the reaction. It has the same units as the reaction velocity (V). It is the highest reaction rate that can be achieved at saturating substrate concentrations.
- [S] is the substrate concentration. It can be expressed in many different forms such as pM, nM, μM, mM, M, ng/mL, %, etc.
- K0.5 is the half-maximal concentration constant. It may also be referred to as Khalf. It is the substrate concentration that gives rise to a reaction velocity that is 50% of Vmax. K0.5 provides useful information about the "apparent affinity" of the protein under study (enzyme, transporter, etc.) for the substrate. Affinity can be thought of as how tightly the substrate binds to the enzyme or transporter protein. The lower the numerical value of K0.5, the higher the apparent affinity for the substrate (i.e., it takes a lower substrate concentration to reach 50% saturation). Conversely, the higher the numerical value of K0.5, the lower the apparent affinity for the substrate (i.e., it takes a higher substrate concentration to reach 50% saturation). If the value of the Hill coefficient is set to 1 (n = 1), K0.5 will be the same as the Michaelis constant (Km) (see Michaelis-Menten equation).
- n is the Hill coefficient. The Hill coefficient is unitless. It provides a measure of the cooperativity of substrate binding to the enzyme, transporter, etc. If n > 1, the reaction/process is thought to exhibit positive cooperativity with respect to substrate binding to the protein. A value of larger than 1 for the Hill coefficient (n > 1) also suggests that there are more than one substrate binding sites in the protein under study. This could arise from the presence of two or more substrate binding sites in a protein monomer. It could also arise from the assembly of multiple subunits of a protein, each with a single substrate binding site. Positive cooperativity refers to the fact that the binding of one substrate facilitates the binding of another substrate to the protein. If n = 1, the Hill equation is reduced to its more familiar form known as the Michaelis-Menten equation. When n = 1, there is no cooperativity with respect to substrate binding to the protein. Note that it is possible to have multiple binding sites without exhibiting any cooperativity. In this case n = 1 in spite of the fact that there are more than one substrate binding sites. If n < 1, the reaction exhibits negative cooperativity with respect to substrate binding.
Hill equation - Interactive graph
The interactive graph provided below allows for a good understanding of the Hill equation, how the reaction velocity changes as a function of the substrate concentration, and how changes in Vmax, K0.5 , and n (Hill coefficient) alter the shape of the graph.
Enter appropriate numerical values for the Maximum velocity (Vmax), half-maximal concentration (K0.5), and the Hill coefficient (n) in the cells below. Then use the Add Plot button to generate a plot of reaction velocity versus the substrate concentration based on the Hill equation presented above. An appropriate substrate concentration range will be used automatically. An unlimited number of plots may be added, but only the first twenty plots are assigned unique colors. Optionally, the units may also be entered in the cells available. Any unit label entered will be added to the title for the corresponding axis.
Depending on user preference, the position of Vmax on the y-axis (i.e., Reaction Velocity axis), the position of K0.5 on the x-axis (i.e., Substrate Concentration axis), legends for all plots, and grid lines may be shown on the graph.
After generating a plot, use the top, left gray arrowheads to adjust the y-axis (i.e., Reaction Velocity) scale, and the bottom, right gray arrowheads to adjust the x-axis (i.e., Substrate Concentration) scale. When the Auto Scale feature is checked, the y-axis maximum is set to be equal to the highest Vmax plotted, and the x-axis maximum is set to be equal to five times the highest K0.5 plotted. The auto scale feature is applied automatically for the very first plot generated.
Posted: Wednesday, October 22, 2014